Evaluation of static program features used in MAGEEC

by Gregory Cawthorne on August 11, 2014

I set out to examine our current choice of features to be extracted from benchmarks, using a process called PCA (Principle Component Analysis). I used BEEBS as a source of programs, since it has been designed to represent a large range of different types of programs and would help me evaluate the feature thoroughly.

The features currently used by MAGEEC are as follows:

( ft1) Basic Block Count
( ft2) BB with 1 successor
( ft3) BB with 2 successor
( ft4) BB with > 2 successor
( ft5) BB with 1 predecessor
( ft6) BB with 2 predecessor
( ft7) BB with > 2 predecessor
( ft8) BB with 1 predecessor 1 successor
( ft9) BB with 1 predecessor 2 successor
(ft10) BB with 2 predecessor 1 successor
(ft11) BB with 2 predecessor 2 successor
(ft12) BB with more than 2 predecessors & more than 2 successors
(ft13) BB with less than 15 instructions
(ft14) BB with number of instructions from 15 – 500
(ft15) BB with more than 500 instructions
(ft16) Edges in control flow graph (CFG)
(ft17) Critical Edges in CFG
(ft18) Abnormal Edges in CFG
(ft19) Conditional Statements
(ft20) Direct Calls
(ft21) Assignments in method
(ft22) Integer operations
(ft23) Floating Point Operations
(ft24) Total Statement in Basic block (BB)
(ft25) Avg Statement in BB
(ft26) Avg phis at top of BB
(ft27) Average phi arguments (args) count
(ft28) BB with 0 phi nodes (phis)
(ft29) BB with 0 – 3 phis
(ft30) BB with more than 3 phis
(ft31) BB phis with greater than 5 args
(ft32) BB phis with 1 – 5 args
(ft33) Switch stmts in method
(ft34) Unary ops in method
(ft35) Pointer Arithmetic
(ft39) Indirect Calls
(ft42) Calls with pointer args
(ft43) Calls with more than 4 args
(ft44) Calls that return float
(ft45) Calls that return int
(ft46) Unconditional branches

I shall be referring to these features as 1-41 — note the gaps — the (ft##) number refers to the order it came in the MILEPOST research paper.

Principle Component Analysis

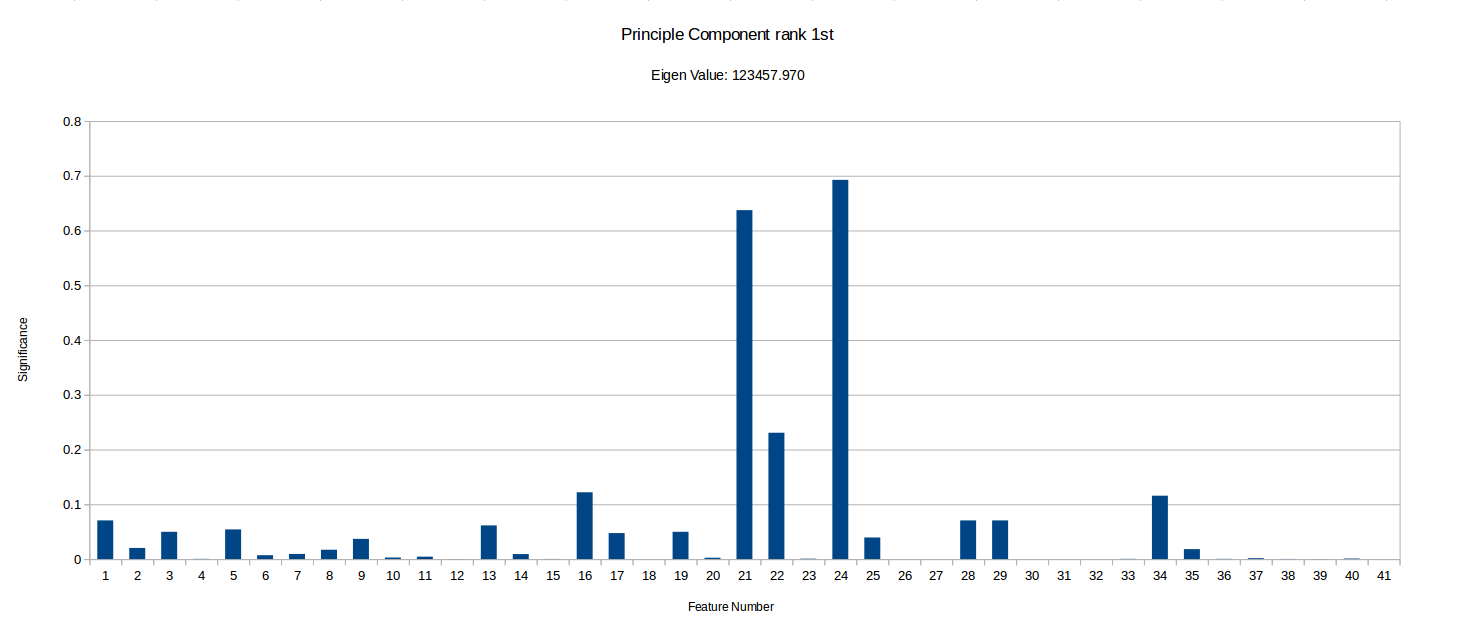
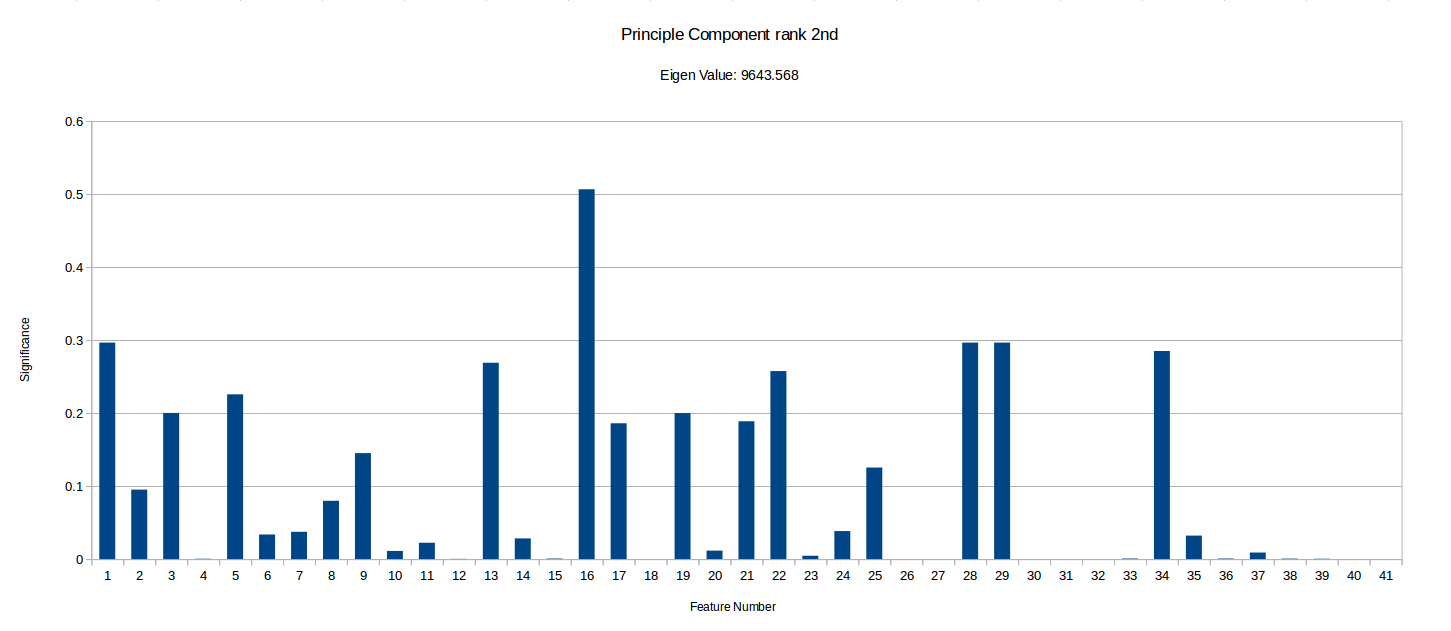
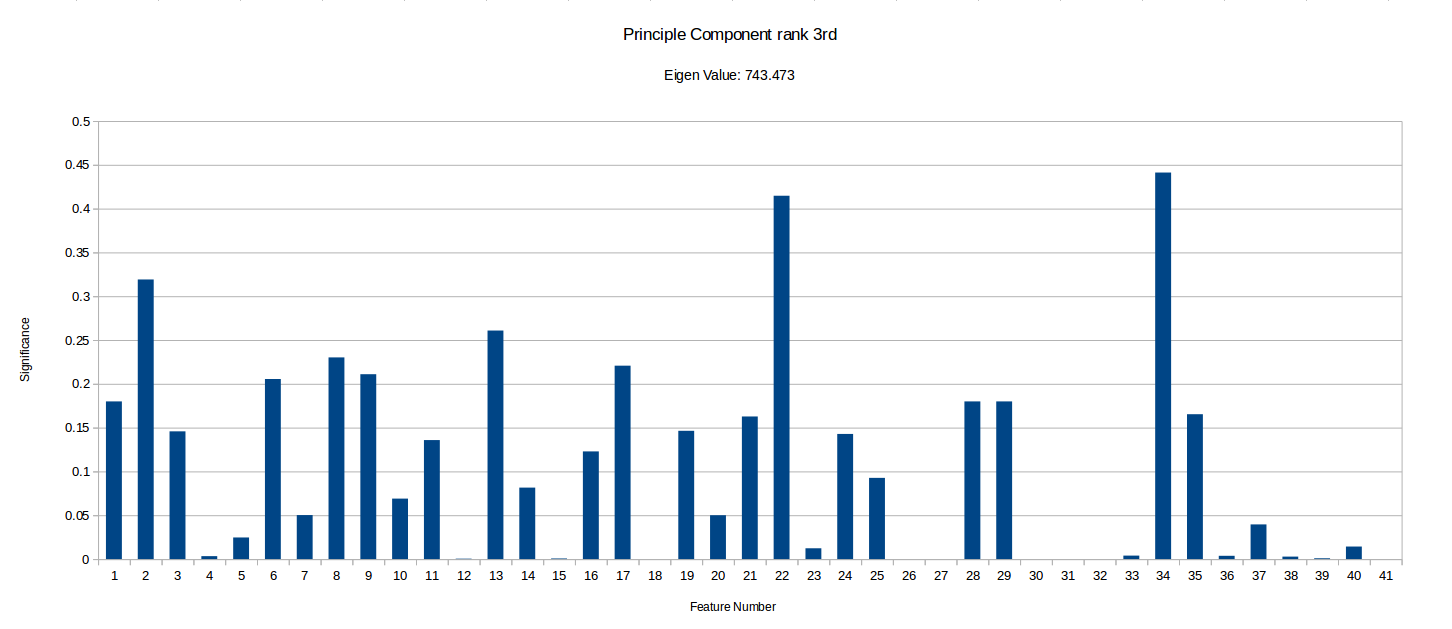
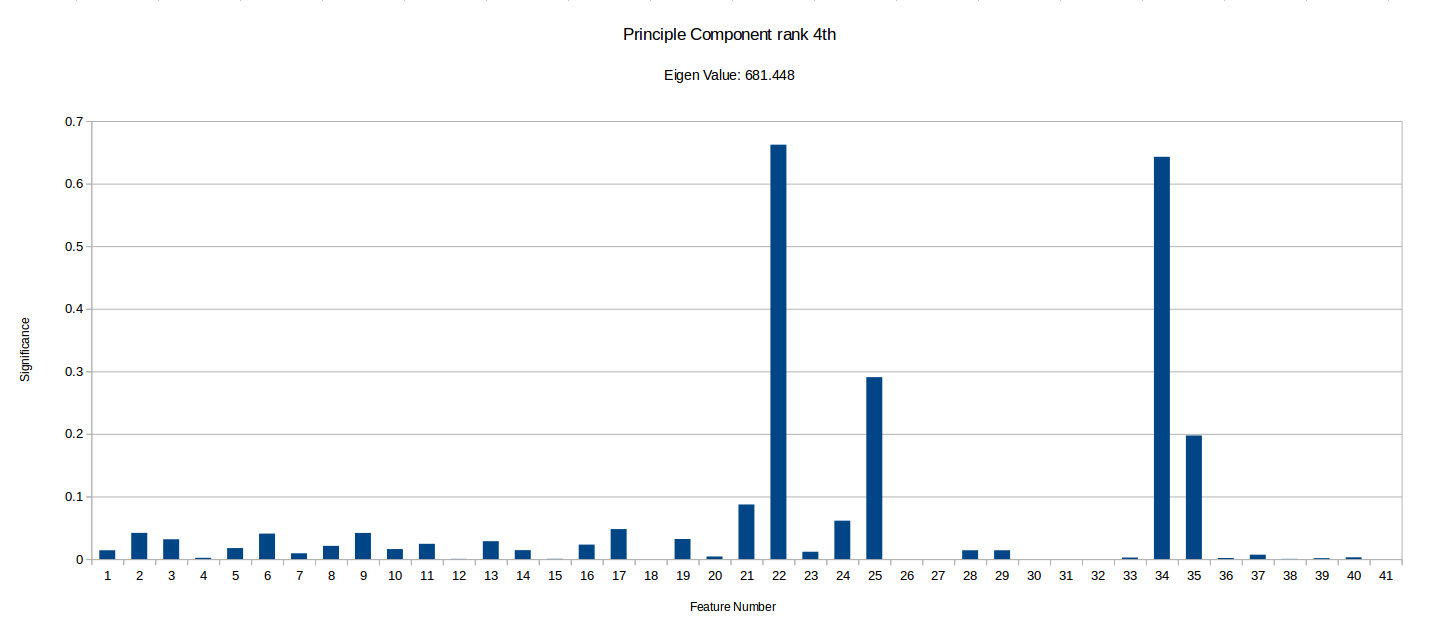
I first ran the feature extractor on every *.c file in the benchmark suite and the fed the data into a PCA program I had designed. The process returns n principle component vectors, where n in the number of features you’re evaluating and each vector is weighted by a score which correlates to how prominent that vector is in the data and how much variation is represents. This process is extremely useful as it becomes very challenging to use any kind of intuition when working with a large number of dimensions.

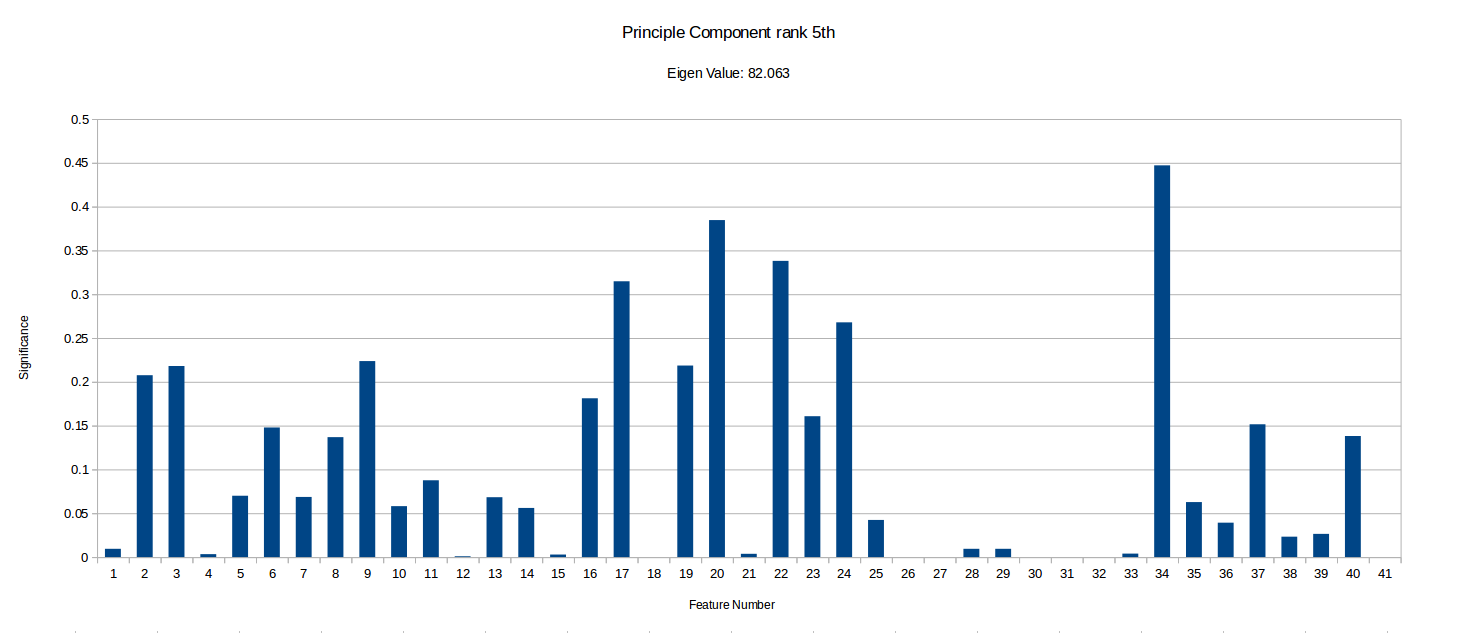
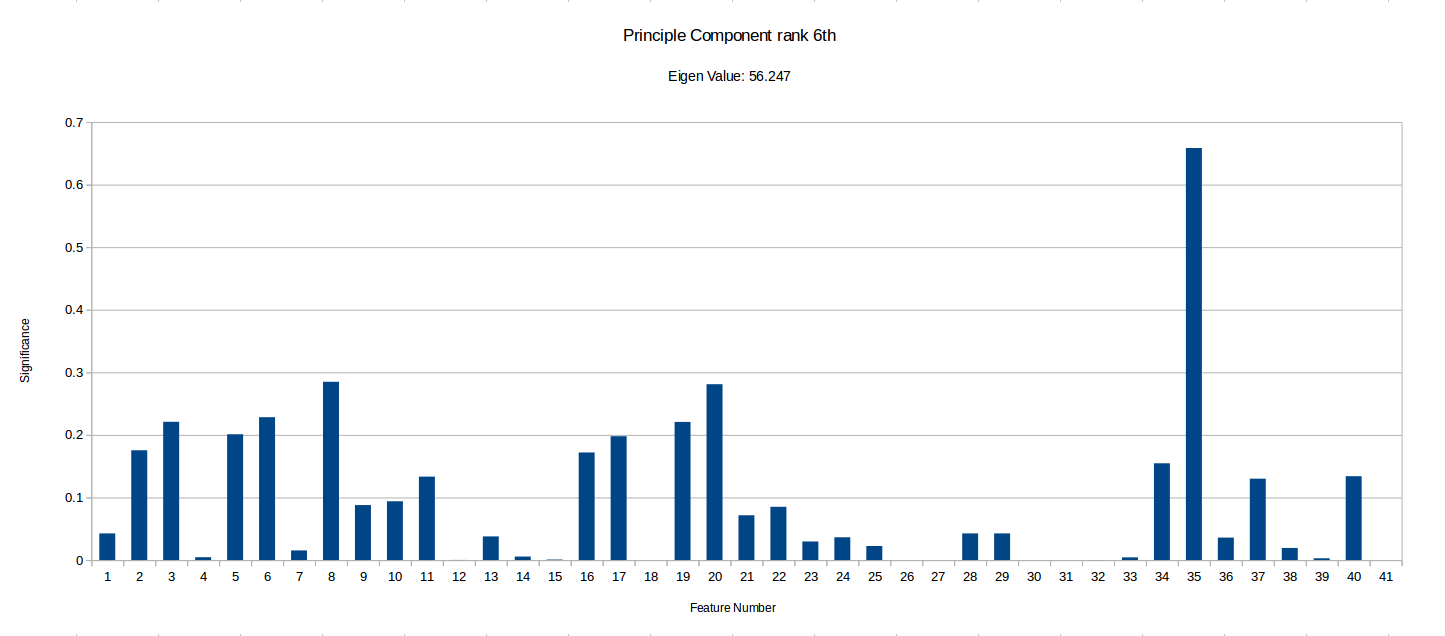
I have ranked the following graphs in terms of the importance of vector. Low significance values for a given feature represents that the feature contributes very little to that component of the data.

It is important to notice that this PCA process can tell us how much certain features vary across the benchmark suit and can therefore ‘hint’ if they are useful in characterising benchmarks, but it doesn’t take into account any energy reading experiments/data and so isn’t fully conclusive. There may be some data which varys only slightly and so is shown as less significant in PCA, but that small variation could be a key factor in energy optimisation.

Vectors

Click any of the below graphs to view a larger version.

N.B. I made all the the dimensions in the vectors positive to make comparing significance of feature easier. Further understanding could possibly be gained by looking at the raw data: PrincipleComponents (underneath the raw data is the same data, but with all of the values >= 0 for use in graph generation)

Notice how the highest value is ~12300, while the smallest I’ve included is ~56. There were also vectors with eigen values as low as -5.578E-14, but I have disregarded these as statistical noise, but they may be components unique to a small subset of the benchmarks. More PCA could be done with more programs focusing on specific types of benchmarks to see if the any of the less significant component vectors are actually more than just noise . Another interesting observation I made is that when I ran the PCA with randomised inputs the eigen values ranged from ~650-1050 with an even spread, while our benchmark produced ~0-123000, with 32 vectors having a eigen value too low (below 20) to deem significant and 4 vectors with eigen values above 100. This implies that there definitely at least a few strong combinations of features in our current feature vector which characterise our programs well.

However, we have highlighted some potentially unimportant features such as 18 (Number of abnormal edges in control graph), 26 (Average number of phi nodes at start of basic block) and 27 (Average Number of arguments for a phi node), which rarely have any significance in the most important components. Although it is important to that PCA does not take into account any energy reading data. These types of hypothesis can be tested by removing them from MAGEEC and running experiments to see if performance is effected.